Melakukan Uji Reliabilitas dengan R
posted to R on 15 March 2017
Jadi udah beberapa hari ini tidak melakukan update post, sebelumnya ada ide tentang menulis artikel perangkat lunak namun jadi buntu karena belum berhasil meng anu kannya. Sekarang karena lagi asyik bermain dengan data maka saya mau menulis tentang uji reliabilitas. Buat yang belum tahu tentang uji reliabilitas ini adalah uji yang dilakukan setelah uji validitas, umumnya uji ini sering menggunakan rumus
- Alpha Cronbach
- Spearman Brown
- Kristoff
- Angoff
- Rullon
Umumnya uji reliabilitas ini menggunakan kuesioner untuk mengukur konsistensi responden dalam menjawab, uji ini dapat dilakukan bersama terhadap seluruh pertanyaan yang diajukan. Seperti yang sudah disampaikan sebelumnya uji ini hanya dilakukan pada butir pertanyaan yang telah melalui uji validitas, pengukuran pada dasarnya bisa dilakukan dengan cara :
- Repeated Measure
Disini sebuah pertanyaan akan disodorkan kembali pada waktu yang berbeda, kemudian dilihat apakah responden masih konsisten dengan jawabannya. - One Short
Disini pertanyaan hanya diajukan sekali untuk kemudian dibandingkan dengan hasil pertanyaan yang lain.
Sebagai acuan umumnya
- Jika nilai Cronbach’s Alpha > 0.60 maka reliabel
- Jika nilai Cronbach’s Alpha < 0.60 maka tidak reliabel
Contoh Kasus
Seorang member dari grup telegram Pegelinux membuat sebuah penelitian dengan menggunakan skala untuk mengetahui kualitas dari static site generator dengan menggunakan skala likert, yaitu:
- Angka 1 = sangat tidak setuju
- Angka 2 = tidak setuju
- Angka 3 = setuju
- Angka 4 = sangat setuju
Kuesioner dibagikan kepada 10 responden, dan didapatkan hasil sebagai berikut
| Responden | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | Q8 | Q9 | Q10 | |
| 1 | 4 | 4 | 3 | 4 | 4 | 3 | 3 | 3 | 3 | 3 |
| 2 | 4 | 3 | 3 | 4 | 3 | 3 | 3 | 3 | 3 | 3 |
| 3 | 2 | 2 | 1 | 3 | 2 | 2 | 3 | 1 | 2 | 3 |
| 4 | 3 | 4 | 4 | 3 | 3 | 3 | 4 | 3 | 3 | 4 |
| 5 | 3 | 4 | 3 | 3 | 3 | 4 | 3 | 4 | 4 | 3 |
| 6 | 3 | 2 | 4 | 4 | 3 | 4 | 4 | 3 | 4 | 4 |
| 7 | 2 | 3 | 3 | 4 | 4 | 4 | 3 | 4 | 2 | 3 |
| 8 | 1 | 2 | 2 | 1 | 2 | 2 | 1 | 3 | 2 | 2 |
| 9 | 2 | 2 | 3 | 3 | 4 | 2 | 1 | 1 | 4 | 4 |
| 10 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 3 | 3 |
Input data ke R dengan menggunakan perintah
> ujireliabilitas <- data.frame(q01 = numeric(0), q02 = numeric(0), q03 = numeric(0), q04 = numeric(0), q05 = numeric(0), q06 = numeric(0), q07 = numeric(0), q08 = numeric(0), q09 = numeric(0), q10 = numeric(0))
> ujireliabilitas <- edit(ujireliabilitas)
maka akan tampil R Data Editor seperti berikut
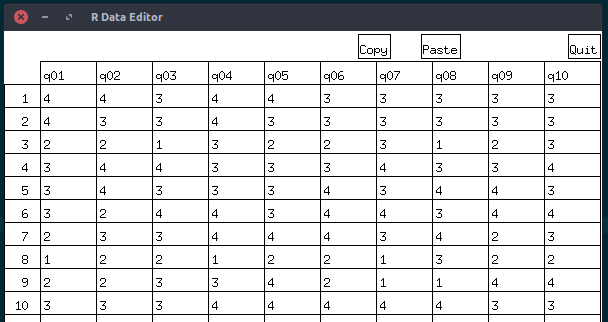
Untuk melakukan analisis reliabilitas kita akan menggunakan fungsi alpha dari library psych, jika kamu belum memilikinya silahkan install dengan perintah
install.packages("psych")
library(psych)
catatan
ggplot2juga memiliki fungsialphajika kamu juga menggunakanggplot2kamu bisa memanggil fungsialphadenganpsych::alpha()
Lakukan analisis dengan perintah berikut
psych::alpha(ujireliabilitas)
Maka akan menghasilkan keluaran sebagai berikut
Reliability analysis
Call: psych::alpha(x = ujireliabilitas)
raw_alpha std.alpha G6(smc) average_r S/N
0.87 0.88 1 0.41 7
Reliability if an item is dropped:
raw_alpha std.alpha G6(smc) average_r S/N
q01 0.85 0.85 0.98 0.40 5.9
q02 0.86 0.87 0.99 0.42 6.6
q03 0.85 0.85 0.99 0.39 5.7
q04 0.85 0.85 0.98 0.39 5.8
q05 0.87 0.87 0.99 0.42 6.5
q06 0.85 0.85 0.99 0.39 5.7
q07 0.86 0.86 0.99 0.41 6.1
q08 0.88 0.87 1.00 0.44 7.0
q09 0.87 0.87 0.99 0.43 6.9
q10 0.88 0.88 0.99 0.44 7.1
Item statistics
r r.cor r.drop
q01 0.77 0.77 0.71
q02 0.64 0.64 0.56
q03 0.82 0.82 0.74
q04 0.79 0.79 0.72
q05 0.66 0.66 0.54
q06 0.81 0.81 0.78
q07 0.72 0.72 0.65
q08 0.56 0.56 0.47
q09 0.57 0.57 0.42
q10 0.53 0.53 0.39
Non missing response frequency for each item
1 2 3 4 miss
q01 0.1 0.3 0.4 0.2 0
q02 0.0 0.4 0.3 0.3 0
q03 0.1 0.1 0.6 0.2 0
q04 0.1 0.0 0.4 0.5 0
q05 0.0 0.2 0.4 0.4 0
q06 0.0 0.3 0.3 0.4 0
q07 0.2 0.0 0.5 0.3 0
q08 0.2 0.0 0.5 0.3 0
q09 0.0 0.3 0.4 0.3 0
q10 0.0 0.1 0.6 0.3 0
Lalu bagaimana membacanya?
raw_alphaadalah apa yang kita sebut Cronbach’s Alpha, karena nilainya lebih dari 0.6 maka mengindikasikan bahwa data tersebut reliabelstd.alphasebenernya mirip denganraw_alpha, tapi saat ini kita hanya perluraw_alphaG6adalah Guttman’s Lambda 6average_radalah rata-rata korelasi antar item (digunakan untuk menghitungstd.alpha)meanskala meansdskala sd
Selain itu yang perlu dianalisa adalah nilai alpha dari masing-masing item, jika nilanya kurang dari raw_alpha bisa dinyatakan bahwa item tersebut perlu dilakukan perbaikan. Dari data diatas diketahui bahwa item 1, item 2, item 3, item 4, dan item 6 memiliki nilai alpha lebih rendah dari raw_alpha. Hal ini berarti bahwa item 5, item 7, item 8, item 9, dan item 10 adalah reliabel, sehingga dapat digunakan untuk pengujian selanjutnya.